ggplot2で3Dプロットする

この記事について
R言語におけるグラフィックスのデファクトスタンダードともいえるggplot2ですが、標準的な機能としてはZ軸の扱いには対応していません。そのため、Rで3D表現を含むグラフなどを作成するには、rglやplotlyなどを使うのが一般的です。
一方で、ggplot2では3次元空間を表現することはできないのかというと、べつにそんなことはなく、やろうと思えばできます。
というか、考えてみてほしいのですが、私たちがいわゆる3D表現だと思って見ているグラフィックスだって、それを表示しているディスプレイは平面ですからね。もちろん、どこまでやれば3D表現といってよいのかという観点はあるものの、極端な話、平面上に3次元空間を投影することさえできれば、ggplot2だろうが、baseのプロットだろうが、3D表現をやることは可能です。
この記事では、透視投影変換などをRで実装したコードを見せたうえで、それを使いつつ、ggplot2で簡単な3D表現をしている例を紹介します。やっていることとしては、次のブログ記事と似たようなことです(これは平行投影の例みたいだけど)。
この記事で紹介するコードをパクると、イメージとしては、たとえば次のようなアニメーションがRでつくれるようになります。
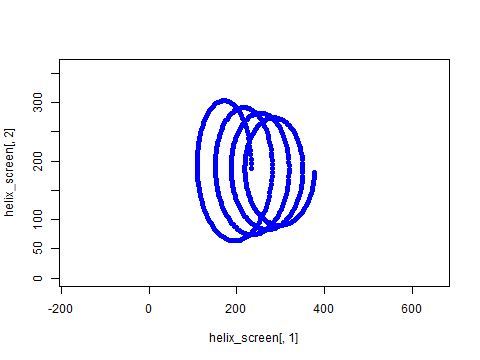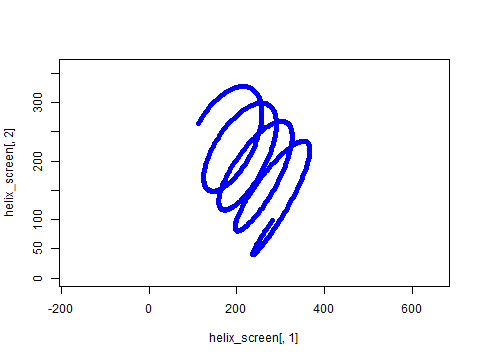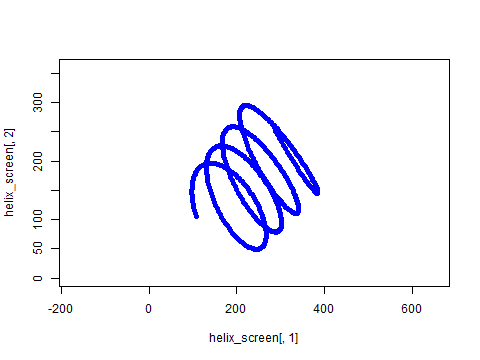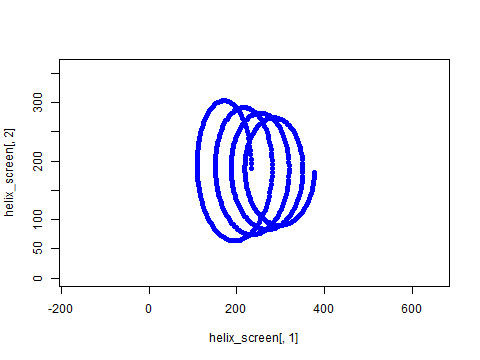
本当にR言語で3D表現したいの…?
とはいえ、ちょっと立ち止まって考えてみましょう。本当に、わざわざR言語で、3D表現を含むようなグラフをつくりたいものでしょうか?
それが技術的にできるというのと、実際にそれができてうれしいかというのは、往々にして別の話だろうと思います。Rで3D表現をしたいようなシーンというのは、たとえば、どんな図をつくりたい場面なのでしょう?
まず考えられるのは、立体的な表現を含むグラフを描きたいという場面かもしれません。Excelとかでつくれそうな、3Dっぽい円グラフとか棒グラフとかのイメージです。しかし、よく言われることですが、一般的な円グラフや棒グラフにパースを付けた表現は、値や割合などを誤解なく読み取ることが難しくなるため、あまり便利なものではないと思います。もちろん、あえてミスリードを誘いたいという場面もなくはないでしょうが、そういう図をわざわざR言語でつくる必要はないかなという気はします。
あるいは、3Dの棒グラフについては、地図上に棒グラフを突き立てたような表現なんかは、天気予報の降水量の表現などで目にすることがあります。ああいうのは、それ系のJavaScriptのライブラリをラップしているパッケージを使うと、Rでもウィジェットとしてつくれたりします。参考までに、そうした表現は次のスライドのなかで試してみています(あまりスマートな例ではありませんが)。
ただ、こういう図の「高さ」については、色を使っても表現できるので、見せ方によっては、とくにこれにこだわる必要はないかもしれません。
もうひとつ考えられるのは、データを3次元空間として可視化することで、そのデータの構造を確認したいといった場面でしょう。こうしたシーンでR言語で描きたくなるような図としては、3次元空間上での散布図と、曲線や曲面をプロットするような図が考えられそうです。
あらかじめ断っておくと、こうした場面ではふつう、グラフをインタラクティブに操作できたほうがむしろ便利なため、rglやplotlyを使っておくのがよいです。
一方で、あえてggplot2なんかで「3D表現ができたらいいのになぁ」と考えるのは、インタラクティブにデータを確認したいというよりは、3次元空間上でのデータを可視化した図表が画像としてほしいというような場面だと思います。論文やレポートのような文書内に挿入する図表を用意したいとか、次のようなアニメーションのコマを用意したいとか、そういうケースです。
raggパッケージでAnimatedを含むWebP画像が書き出せるようになったので試してみた。gifskiほど爆速ではないけど、これはグラフィックデバイスなので、画像ファイルを一時的に書き出さずにインメモリでアニメーションを出力できる。R言語的には画期的だと思うhttps://t.co/bEzcaQfdQU pic.twitter.com/u2z5g7M0VU
— あきる (@paithiov909) September 6, 2025
座標変換のためのRコード
こういうのはどうやってやるのかというと、冒頭に書いたように、元のデータから座標を変換したりするとできます。座標変換についてきちんと説明するのは私の手に余るのでここで詳しくは説明しませんが、参考までに、3次元の座標変換については、次の記事を読むとだいたいわかりそうです。
R言語ユーザー向けにとてもざっくりいうと、データをn行4列(XYZ列と、すべての値を1で埋めたW列)の行列として持っておいて、その行列に適当な変換行列をかけたりすると、データを平面に投影できるという話です。変換行列を用意するための関数は次のような感じで書けます。コメントもそのままコピペしているので、使い方はコメントを読んで察してください。
#' @noRd
vec3_normalize <- function(v) {
mag <- sqrt(sum(v^2))
v / mag
}
#' @noRd
vec3_cross <- function(a, b) {
c(
a[2] * b[3] - a[3] * b[2],
a[3] * b[1] - a[1] * b[3],
a[1] * b[2] - a[2] * b[1]
)
}
#' @noRd
as_trans3d <- function(m) {
class(m) <- unique(c("transform3d", "at_matrix", class(m)))
m
}
#' Perspective division
#'
#' Multiplication of two matrices after normalizing the first one.
#'
#' @param lhs,rhs Numeric matrices.
#' @returns A numeric matrix.
#' @keywords internal
#' @export
#' @rdname ndc_mul
ndc_mul <- function(lhs, rhs) UseMethod("ndc_mul")
#' @export
ndc_mul.default <- function(lhs, rhs) {
w <- lhs[, 4]
ok <- w != 0 & is.finite(w)
if (!all(ok)) {
rlang::warn("Some points had invalid w (0, NA, or Inf). They were dropped.")
}
lhs[ok, 1:3] <- lhs[ok, 1:3] / w[ok]
lhs[ok, 4] <- 1
lhs[ok, ] %*% rhs
}
#' @export
ndc_mul.transform3d <- function(lhs, rhs) {
rlang::abort("`lhs` must be a numeric matrix")
}
#' @keywords internal
#' @export
#' @rdname ndc_mul
`%!*%` <- ndc_mul
#' 3D world to camera transformation
#'
#' @param eye A numeric vector of length 3 giving the position of the camera.
#' @param center A numeric vector of length 3 giving the position where the camera is looking at.
#' @param up A numeric vector of length 3 giving the direction of the "up" vector for the camera.
#' @param fovy A numeric scalar giving the field of view in radians.
#' @param aspect A numeric scalar giving the aspect ratio.
#' @param near A numeric scalar giving the distance to the near plane.
#' @param far A numeric scalar giving the distance to the far plane.
#' @param width,height A numeric scalar giving the width and height of the viewport.
#' @param ox,oy A numeric scalar giving the offset of the viewport in pixels.
#' @returns A `transform3d` object.
#' @rdname camera
#' @name camera
NULL
#' @rdname camera
#' @export
lookat3d <- function(eye, center, up = c(0, 1, 0)) {
if (!all(eye != center)) {
msg <- glue::glue(
"`center` must be different from `eye` for all dimensions. Found same values at positions: {paste0(which(eye == center), collapse = ', ')}"
)
rlang::abort(msg)
}
z <- vec3_normalize(center - eye)
x <- vec3_normalize(vec3_cross(z, up))
y <- vec3_normalize(vec3_cross(x, z))
# fmt: skip
out <- matrix(
c(
x[1], y[1], z[1], -x %*% eye,
x[2], y[2], z[2], -y %*% eye,
x[3], y[3], z[3], -z %*% eye,
0, 0, 0, 1
),
ncol = 4,
byrow = TRUE
)
as_trans3d(t(out))
}
#' @rdname camera
#' @export
persp3d <- function(fovy, aspect, near = 0.1, far = 10) {
if (far <= near) {
rlang::abort("`far` must be greater than `near`")
}
if (near <= 0) {
rlang::abort("`near` must be greater than 0")
}
f <- 1 / tan(fovy * .5)
# fmt: skip
out <- matrix(
c(
f / aspect, 0, 0, 0,
0, f, 0, 0,
0, 0, (far + near) / (near - far), 2 * far * near / (near - far),
0, 0, -1, 0
),
ncol = 4,
byrow = TRUE
)
as_trans3d(t(out))
}
#' @rdname camera
#' @export
viewport3d <- function(width, height, ox = 0, oy = 0) {
# fmt: skip
out <-
matrix(
c(
width / 2, 0, 0, width / 2 + ox,
0, -height / 2, 0, height / 2 + oy,
0, 0, .5, .5,
0, 0, 0, 1
),
ncol = 4,
byrow = TRUE
)
as_trans3d(t(out))
}
これらの関数はrasenganという自作Rパッケージに導入しているので、それをインストールすれば使えます。あるいは、大した行数じゃないので、上のコードブロックをコピペして使ってもいいと思います。その場合、glueパッケージとrlangパッケージに依存している点にだけ注意してください。
3次元での曲面の描画
試しに使ってみましょう。おしり曲面というのを点群として描画してみることにします。そんな曲面、知らないですもんね。本当におしりのような形になるのか、確認してみます。
この曲面は、なんかこんな感じの式で与えられるらしいです。
f <- \(x, y, d = 5) {
# 1/8* (6*exp(-((2/3*abs(x) - 1)**2 + (2/3 *y)**2) - 1/3*(2/3*y + 1/2)**3)+ 2/3 *exp(-2.818**11*((abs(2/3*x) - 1)**2+ (2/3 *y)**2)**2) + 2/3*y - (2/3*x)**4)
1 / d * (6 * exp(-((2 / 3 * abs(x) - 1)**2 + (2 / 3 * y)**2) - 1 / 3 * (2 / 3 * y + 1 / 2)**3) + 2 / 3 * exp(-2.818**11 * ((abs(2 / 3 * x) - 1)**2 + (2 / 3 * y)**2)**2) + 2 / 3 * y - (2 / 3 * x)**4)
}
Pythonのコードをコピペしているので^になるべきところが**になっていますが、R言語は歴史的な経緯から**でも累乗できることになっているので、実はこのまま使えます。
これをもとに、曲面を描くためのデータを作る関数を用意します。ここではouter()を使って、格子点p上のf()の値を計算しています。pの値の範囲は、なんかそれっぽい見た目になるように適当に決めています。
oshiri_dat <- \(n = 300, trans = FALSE) {
p <- seq(-pi * 4 / 5, pi * 4 / 5, length.out = n)
z <- outer(p, p, f) |>
as.vector()
dplyr::tibble(
id = rep(seq_len(n), each = n),
d = tidyr::expand_grid(x = p, y = p) |>
dplyr::mutate(
z = if (trans) log(abs(z)) else z,
w = 1
) |>
as.matrix()
)
}
で、これを次のようにしてggplot2で描画するためのデータをつくります。%!*%は、いわゆる透視除算というやつをするために定義した演算子です。
use("rasengan", "%!*%")
mat <-
affiner::transform3d() %*%
affiner::scale3d(1.5, 1.5, 1.5) %*%
rasengan::lookat3d(c(4, 8, 6), c(0, 0, 0)) %*%
rasengan::persp3d(pi / 4, 720 / 576)
dat <-
oshiri_dat(trans = TRUE) |>
dplyr::mutate(
d = d %*% mat %!*% rasengan::viewport3d(720, 576)
)
このデータはたとえば次のようにしてプロットできます。raggでキャプチャするときにグラフィックデバイスのサイズも720x576にしていますが、ggplot2などはプロットエリアがグラフィックデバイスのサイズいっぱいに描画されるわけではないので、ここはビューポートと同じサイズである必要はないです。
library(ggplot2)
cap <- ragg::agg_capture(width = 720, height = 576)
ggplot(dat) +
geom_point(aes(d[, 1], d[, 2], size = d[, 3], alpha = d[, 3]), color = "navy") +
scale_size(range = c(0, 1)) +
scale_alpha(range = c(0, 1)) +
scale_color_identity() +
coord_cartesian(xlim = c(0, 720), ylim = c(0, 576)) +
theme_minimal() +
theme(
legend.position = "none",
plot.margin = unit(c(0, 0, 0, 0), "cm")
)
rast <- cap(native = TRUE)
dev.off()
#> agg_png
#> 2
grid::grid.newpage()
grid::grid.raster(rast, interpolate = FALSE)
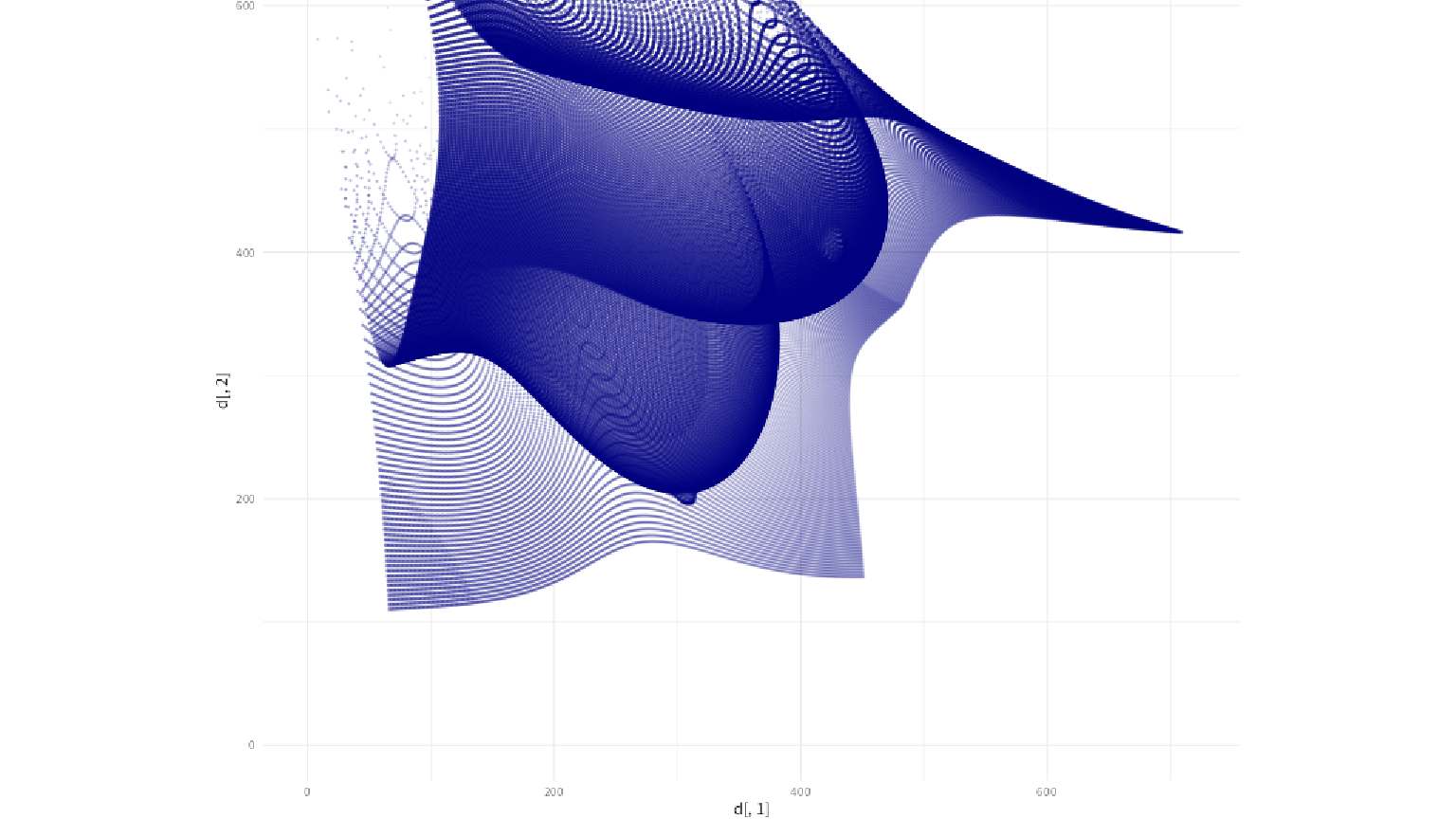
これが「おしり」かといわれると、よくわからないですけど、とりあえず描画はできることがわかります。
3次元での曲線の描画
同様にして、曲線も描画してみましょう。
ここでは、いわゆる「ローレンツ・アトラクター」というやつを描いてみます(次のような方程式の解らしいので、deSolveを使って求解しているが、パラメータがわかっていれば漸化式っぽく書けるので、それでよかったかも)。
lorenz_eq <- \(t, y, params, ...) {
with(params, {
dy1 <- sigma * (y[2] - y[1])
dy2 <- rho * y[1] - y[2] - y[1] * y[3]
dy3 <- y[1] * y[2] - beta * y[3]
list(c(dy1, dy2, dy3))
})
}
params <- list(sigma = 10, beta = 8 / 3, rho = 28)
init_state <- c(x = -2.29209, y = 0.098299, z = 24.50526)
attractor <-
deSolve::ode(init_state, seq(0, 100, 0.01), lorenz_eq, params)
これをもとにして、次のように曲線のデータをつくります。カメラの位置などは雰囲気で適当に設定しています。ggplot2::geom_curve()を使うために、dplyr::lag()を使って、一つ後ろの点を表すx2とy2をつくっておくのがポイントです。
dat <-
(cbind(attractor[, 2:4], 1) %*%
affiner::transform3d() %*%
affiner::scale3d(1.5, 1.5, 1.5) %*%
rasengan::lookat3d(c(0, 4, -12), c(.3, .3, .3)) %*%
rasengan::persp3d(pi / 4, 720 / 576) %!*%
rasengan::viewport3d(720, 576)) |>
dplyr::as_tibble(.name_repair = ~ c("x", "y", "z", "w")) |>
dplyr::mutate(
x2 = dplyr::lag(x, default = dplyr::last(x)),
y2 = dplyr::lag(y, default = dplyr::last(y))
)
これを、こうするとプロットできます。
cap <- ragg::agg_capture(width = 720, height = 576)
ggplot(dat) +
geom_curve(
aes(x, y, xend = x2, yend = y2, color = z),
alpha = .6,
curvature = .01
) +
coord_cartesian(xlim = c(0, 720), ylim = c(0, 576)) +
theme_minimal() +
theme(
legend.position = "none",
plot.margin = unit(c(0, 0, 0, 0), "cm")
)
rast <- cap(native = TRUE)
dev.off()
#> agg_png
#> 2
grid::grid.newpage()
grid::grid.raster(rast, interpolate = FALSE)
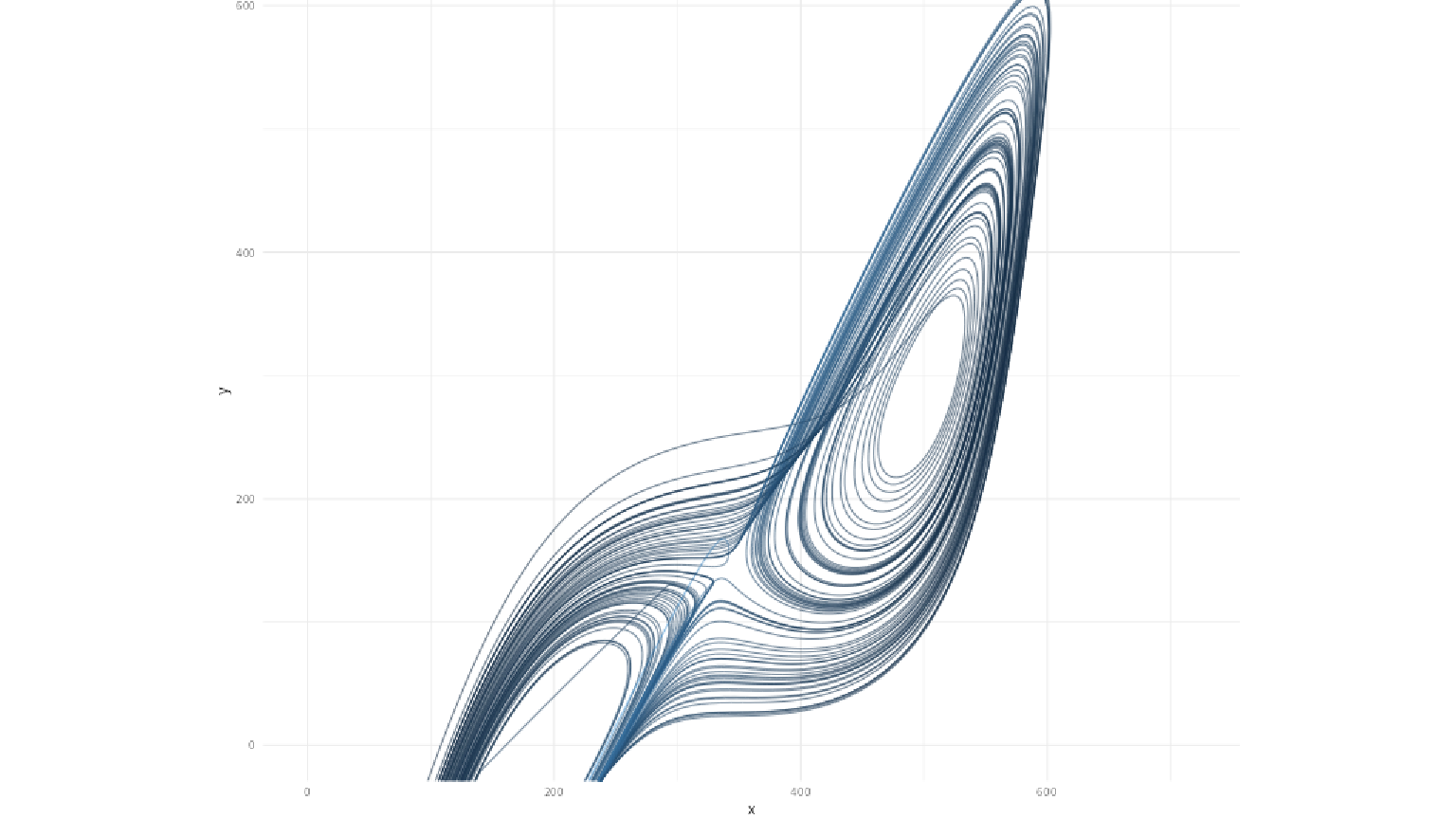
むすび
注意点として、この記事で紹介したようなやり方で座標変換した場合、ggplot2の側の軸の目盛りは元のデータとは対応しなくなっているため、目盛りから何かを読み取るようなことはできません。自分で軸や目盛りもグラフ中に描いてしまえばよいのですが、そこまではしない場合、あくまでデータの大まかな形状を把握するような用途でしか使えない点に注意が必要です。まあ、だからふつうは、rglとかのほうが便利だと思います。素直にrglを使いましょう。
また、視点(カメラ)を用意したり、パースを付けたりする必要がない場合、affinerパッケージだけを使って平行投影するのでも、投影すること自体は可能です。次のような感じです。
affinerを使えば3次元空間の軸を回転できるのを覚えたので、素のggplot2でも3Dプロットみたいなことができるはずではと思ってやってみた図 pic.twitter.com/0Kw2SKg6nT
— あきる (@paithiov909) June 13, 2025
ggplot2などに座標変換したデータを持ち込む場合、そもそもプロットされる範囲はデータの範囲に応じていい感じに調整されるはずなので、透視投影変換・透視除算・ビューポート変換までするのは、目的によってはちょっと大げさかもしれません。そのあたりは空気を読んで、適切と思われるやり方で試してみるとよいでしょう。
